理解浅层神经网络
首先介绍一本书,刚看了一点,感觉讲的挺好的,understand deeplearning
单输入单输出可视化
首先考虑一个函数:$\begin{aligned}
y & =\mathrm{f}[x, \boldsymbol{\phi}] \
& =\phi{0}+\phi{1} \mathrm{a}\left[\theta{10}+\theta{11} x\right]+\phi{2} \mathrm{a}\left[\theta{20}+\theta{21} x\right]+\phi{3} \mathrm{a}\left[\theta{30}+\theta{31} x\right] .
\end{aligned}$
如果稍微了解过神经网络算法的就能明白这是一个两层的分类器。
我们假设a[*]是ReLU激活函数,$\mathrm{a}[z]=\operatorname{ReLU}[z]=\left{\begin{array}{ll}
0 & z<0 \
z & z \geq 0
\end{array} .\right.$
我们可以将上面的函数拆解一下并且进行可视化,可视化结果如下:
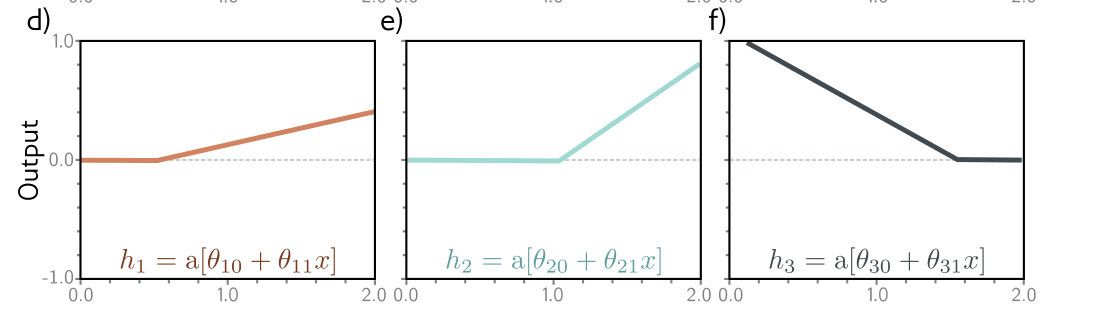
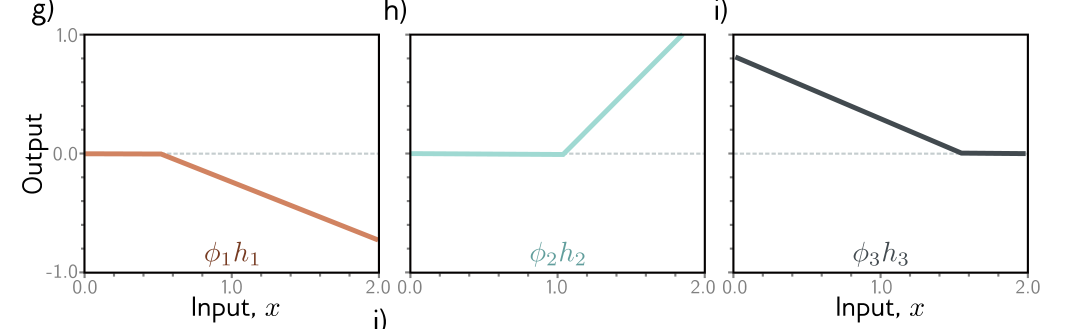
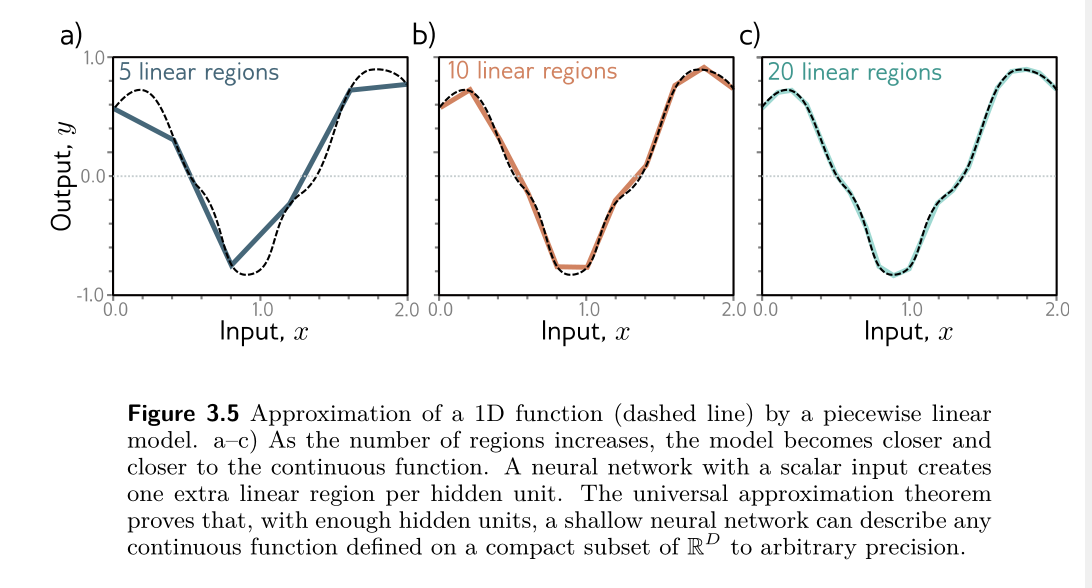
图a-c是数据只经过一次线性变换未激活之前的,图d-f是经过ReLU函数激活之后的,图g-h是又经过了一次线性变换之后的结果,图j是经过最后全连接层也就是图g-h结果相加。稍加分析就可以知道,由于隐藏单元数量的影响,无论参数怎么变化,最后得到的结果只能有四个区域,每添加一个隐藏单元,就会在结果上添加一个线性区域。实际上,经过普遍逼近原理可以证明,单层的神经网络只要隐藏层足够多可以无限逼近拟合所有函数。
多输入单输出可视化
如果输入不再是标量形式,而是变成向量,那么结果会有所变化吗?
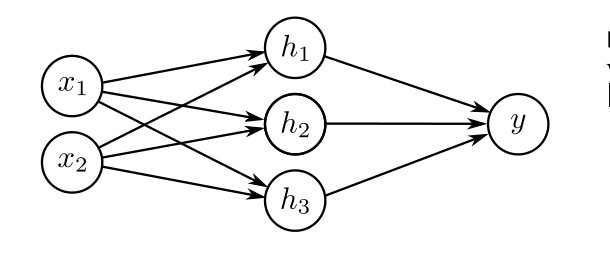
每一层函数可视化结果如下:
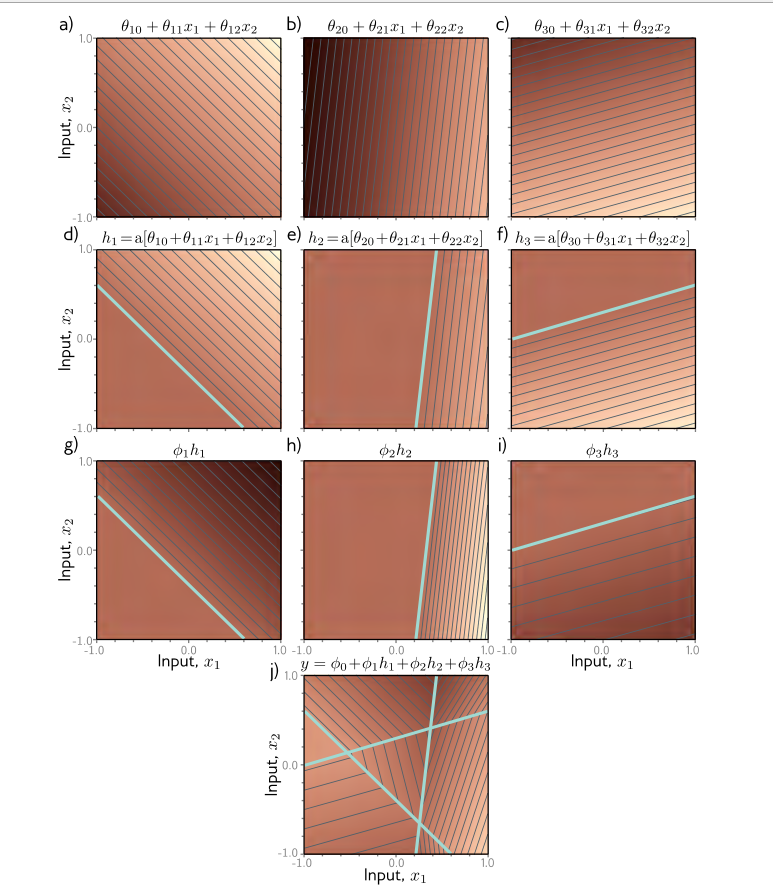
经过分析可以知道,上面的直线被平面给代替了而已,原来二维空间中是直线对空间进行分割,这里只是改成了平面而已。输入维度为2时,隐藏层越多,线性区域的增长速度甚至超过$2^{Di} $。
我们虽然没有办法去想象输入大于2维的情况,但是根据我们的推理可以得到原理基本上是相似的。
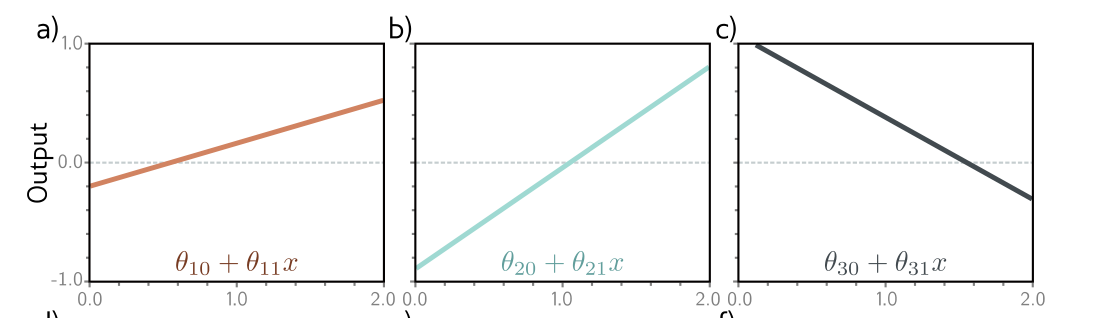
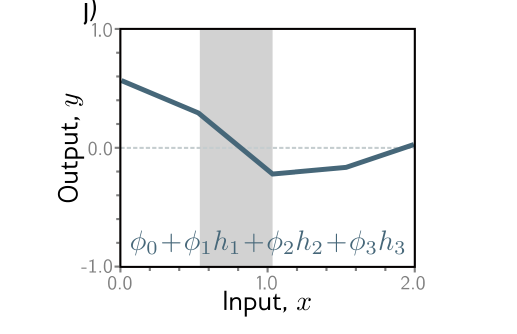
单输入多输出可视化
单输入多输出情况可以看做单输入单输出情况用不同参数跑了两边得到的结果,他们最后得到的线性区域数量是一样的,而且分割的点也一样(因为输入层到隐藏层是共用的)